Intro
Gradient descent(경사 하강법)은 최적화 기법 중 하나로, 손실 함수를 최소화하기 위해서 사용된다. 경사 하강법에선 효과적으로 $\theta$ 를 변화시키기 위해, 가장 가파른 경사 방향으로 $\theta$ 를 업데이트한다. 이때, 가장 가파른 경사일 때의 방향이 Gradient 방향 일 때 이므로, $\theta$ 는 Gradient의 반대 방향으로 업데이트된다.
누군가 나에게 경사 하강법을 간단하게 설명하라고 하면, 아마도 위에 적은 것처럼 말할 거 같다.
근데 저 설명을 듣는 입장에선, 아마도 왜 가장 가파른 경사일 때의 방향이 Gradient 방향이고, 왜 Gradient의 반대 방향으로 $\theta$ 가 업데이트 돼야 하는 지에 대해서 의문이 생길 거 같다.
그래서 위와 같은 궁금증을 해결할 수 있도록, 관련된 내용을 찾아서 정리했다.
'경사 하강법이 Gradient의 반대 방향으로 진행되는 이유'를 확인하기 위해서, 우선 $\theta$ 에 따른 손실 함수의 변화 양상을 살펴볼 것이다. 이후 변화의 방향에 대한 정보를 얻고, 이 정보를 활용해서 $\theta$ 가 어떤 방향으로 이동해야 가장 효과적인지 확인한다.
경사 : 변화량에 대한 정보

우선은 경사라는 표현부터 정리해 보자.
경사라는 표현이 어색할 수도 있지만, 경사는 손실 함수의 평면을 기준으로 변화율을 나타낸 표현이다. 그래서 Gradient 방향이 가장 가파르다는 것은, 해당 방향일 때의 손실 함수 변화율이 가장 크다는 말과 같다.
따라서 앞으론 '가장 가파른 경사'라는 표현 대신, '변화율이 가장 크다'는 표현을 사용한다.
특정 변수에 의한 변화율 확인 : 편미분을 통해서
먼저 '변수에 의한 손실 함수의 변화율'을 확인해 보자.
변화율 정보를 알게 되면, 최종적으로 방향을 찾는데 도움이 될 것이다.
우리가 관심 있는 것은 $\theta$ 와 손실 함수 사이 관계이기 때문에, 결국 $\theta$ 에 의한 손실 함수의 변화율을 확인해야 한다.
손실 함수의 변화율을 구하기 위해선 결국 $d(손실 함수) = f(\theta)d\theta$ 를 계산해야 한다.
손실 함수는 다변수 함수라서 $\theta$ 는 $(\theta_1, \theta_2, \theta_3 ...\theta_n)$ 와 같고, $\theta$ 에 의한 변화율을 구하는 것은 결국, $(\theta_1, \theta_2, \theta_3 ... \theta_n)$ 로 인한 변화율을 구하는 것과 동일하다.
따라서 손실 함수 변화율을 구하려면 다음과 같은 식을 계산해야 할 것이다. 이제 $ㅁ$만 채우면 $\theta$ 에 의한 손실 함수의 변화율을 알 수 있게 됐다!
$$d(손실 함수) = ㅁd\theta_1 + ㅁd\theta_2 + ㅁd\theta_3 + ...ㅁd\theta_n$$
식을 통해서 알 수 있는 것은 $ㅁ$는 모두 $d\theta_i$ 항과 관련 있다는 것이다. 이는 결국 $ㅁ$가 각 $\theta_i$ 방향으로의 변화율 정보를 포함해야 한다는 것을 의미한다.
$\theta_i$ 방향의 변화율 정보라는 것은 결국, '오직 $\theta_i$ 와 손실 함수 사이 만의 관계'이다. 따라서 각 방향에 대한 변화율을 얻기 위해선, 다른 변수들의 영향을 없애야 한다. 이는 $\theta_i$ 를 제외한 다른 변수들은 상수 취급함으로써 가능하다.
실제로 다른 변수를 상수 취급한다면, 아래 그림처럼 $z$에 대해 각 변수마다 다른 접선(순간 변화율) 정보를 얻을 수 있다.
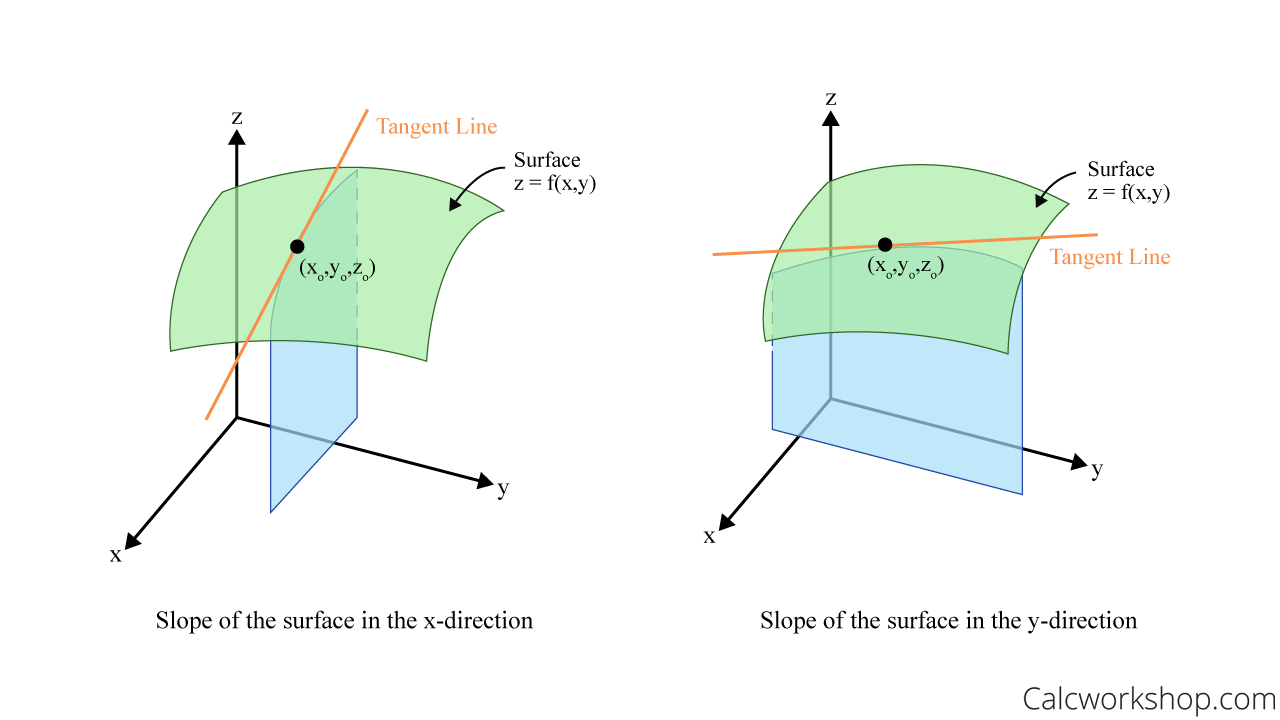
이처럼 다른 변수를 상수 취급한 상태에서, 한 변수에 의한 변화율만 확인하는 것을 편미분(partial derivative)이라고 한다.
변수 1개에 대한 변화율만 고려하는 편미분의 특성은, 편미분의 식을 통해 직관적으로 확인할 수 있다.
실제로 $z = f(x, y)$ 함수에 대한 $x$와 $y$에 대한 편미분을 정의하면 아래와 같은데, 미소 값인 $h$가 특정 변수에만 더해지는 것을 확인할 수 있다. 이는 곧 편미분이 특정 변수에 의한 변화량만 고려한다는 것을 의미한다.
$$f_x(x,y) = \lim_{h\to 0} \frac{f(x+h,y) - f(x,y)}h.$$
$$f_y(x,y) = \lim_{h\to 0} \frac{f(x,y+h) - f(x,y)}h.$$
결국 우리가 궁금했던 각 $\theta_i$ 에 대응되는 $ㅁ$ 엔 편미분이 들어가게 된다. 이에 따라 식을 다시 한번 정리하면 아래와 같다. 이는 최종적으로 변수에 의한 손실 함수의 변화율이 각 $\theta_i$ 방향으로의 편미분으로 표현된다는 것을 의미한다.
$$d(손실 함수) = f_{\theta_1}(\theta)d\theta_1 + f_{\theta_2}(\theta)d\theta_2 + f_{\theta_3}(\theta)d\theta_3 + ...f_{\theta_n}(\theta)d\theta_n$$
변화율의 방향을 확인하기 : Gradient를 통해서
손실 함수의 변화율이 $\theta_i$ 에 대한 편미분으로 표현될 수 있다는 것이 확인 됐으니, 이제는 변화율의 방향 정보만 알면 된다. 변화율의 방향을 알게 되면, 이를 활용해 $\theta$ 의 이동 방향 또한 결정할 수 있다. 다행히 변화율의 방향은 앞서 구한 편미분을 활용하여 쉽게 얻을 수 있다.
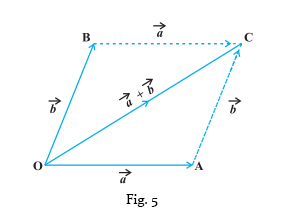
편미분은 오직 $\theta_i$만 변수로 고려하기 때문에, 각 변수에 의한 방향 정보를 표준 기저 벡터 $\vec {e_i}$ (한 성분만 1인 벡터)를 써서 $f_{\theta_i}(\theta) \vec {e_i}$로 나타낼 수 있다. 최종적으로 우리는 모든 변수에 의한 방향 정보가 궁금하기 때문에, 모든 $i$에 대한 $f_{\theta_i}(\theta) \vec {e_i}$ 를 더해서 새로운 벡터를 만들면, 변화율의 방향 정보를 얻을 수 있다.
변화율의 방향 정보를 나타내는 벡터를 계산하면 $\langle f_{\theta_1}(\theta), f_{\theta_2}(\theta), \cdotp\cdotp\cdotp, f_{\theta_n}(\theta) \rangle$와 같은데 이를 부르는 명칭이 바로 Gradient이다. 결국 우리는 Gradient를 통해 $\theta$ 에 의한 손실 함수의 변화 방향과 변화율을 나타낼 수 있게 됐다.
Gradient를 기호를 사용해서 표현하면 아래와 같다.
$$\nabla f=\langle f_{\theta_1}(\theta), f_{\theta_2}(\theta), \cdotp\cdotp\cdotp, f_{\theta_n}(\theta) \rangle$$
Gradient가 변화율의 방향과, 크기를 나타내는 벡터라는 사실을 생각하면, 왜 인터넷에 Gradient를 검색하면 아래와 같이 '평면과 함께 길이가 다른 화살표가 나오는지'를 이해할 수 있게 된다.
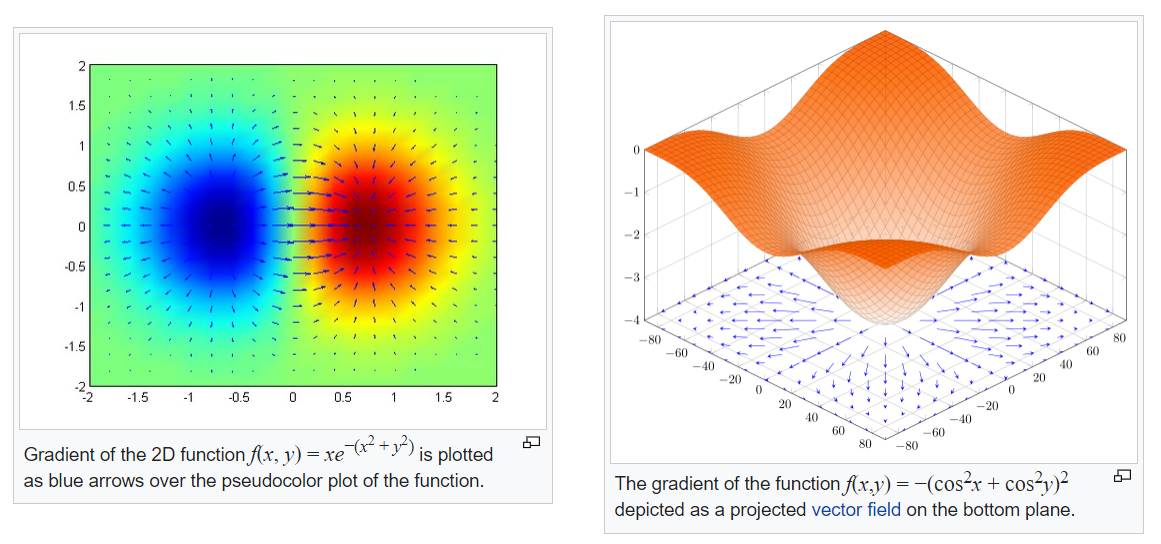
$\theta$ 의 이동 방향 결정 하기 : 방향 도함수를 통해서
Gradient를 활용해서 특정 $\theta$에서의 손실 함수 변화율을 벡터로 표현할 수 있음을 확인 했다. 이제 $\theta$ 가 이동할 방향이 Gradient과 반대여야 한다는 것만 보이면, 경사 하강법이 Gradient의 반대 방향으로 진행되는 이유를 확인할 수 있다.
확인을 위해, 우선 $\theta$ 의 이동 방향에 대해서 생각해보자. 경사 하강법에선 $\theta$ 의 이동에 따라 손실 함수가 감소해야 하고, 또 그 변화 정도가 크면 클 수록 좋을 것이다. 이를 만족하기 위해선 $\theta$ 의 이동 방향이 손실 함수의 최대 감소율 방향이어야 한다.
결국 우리는 $f$ 위의 점에서 임의의 방향 $\vec u$ (크기가 1인 단위 벡터)로의 변화율을 확인해야 하는데, 이때 활용할 수 있는 것이 바로 방향 도함수(directional derivatives)이다.
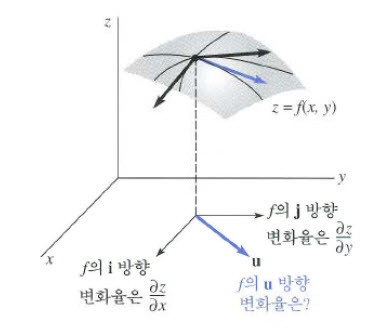
실제로 $f(x, y)$ 의 점에서 $\vec u$ 로의 방향 도함수를 정의하면 아래와 같은데, 식을 살펴 보면 미소 값 $h$ 가 $\vec u$ 의 방향에 더해진 것을 알 수 있다. 이를 통해 방향 도함수가 $\vec u $ 방향의 변화율을 고려한다는 것을 직관적으로 확인할 수 있다.
$$D_{\vec u\,}f(x,y) = \lim\limits_{h\to 0} \frac{f(x+hu_1,y+hu_2) - f(x,y)}h.$$
$\theta$ 의 $\vec u$ 방향에 대한 변화율을 방향 도함수를 통해 표현 했으니, 이제 우리는 방향 도함수가 최소인 경우를 찾아야 한다. 방향 도함수가 최소라면, 손실 함수의 감소율이 최대가 될 것이기 때문이다.
방향 도함수는 $f$ 가 미분 가능한 경우, $D_{\vec u}f = \nabla f\cdot \vec u$ 로 표현할 수 있다는 특징이 있다. 이를 활용하면 방향 도함수를 $\theta$ 의 이동 방향을 나타내는 단위 벡터 $\vec u$ 와 Gradient 사이 내적(inner product)만으로 구할 수 있다.
$\vec u$ 와 $\nabla f$ 의 내적을 통해서 방향 도함수를 나타내면 다음과 같다.
$$D_{\vec u\,}f(\theta) = \vec{u} \cdot \nabla{f} = |\vec{u}| |\nabla{f}| cos \, \phi $$
방향 도함수가 가장 작은 값을 가지려면, $\vec u$ 와 Gradient 사이의 내적 값이 최소가 돼야 한다. 이를 위해선 $cos \, \phi$가 최소여야 하기 때문에, 결국 두 벡터의 사잇각 $\phi$는 $180\,^{\circ}$ 여야 한다.
방향 도함수가 최소일 때의 $\vec u$ 와 Gradient 의 사잇각이 $180\,^{\circ}$ 라는 것은, 결국 $\theta$ 의 진행 방향이 Gradient 방향과 반대일 때 손실 함수가 가장 크게 감소한다는 것을 의미하고, 이것이 바로 경사 하강법의 진행 방향($\theta$ 의 이동 방향)이 Gradient의 반대 방향인 이유이다.
$\phi$ 에 따라 변하는 방향 도함수
임의의 $\vec u$ 와 Gradient 의 사잇각 $\phi$ 에 따라 변하는, 방향 도함수의 성질을 확인하기 좋은 사이트가 있어서 아래에 링크를 남긴다. $\phi$ 를 직접 바꿔가면서 방향 도함수의 변화를 확인하다 보면, Gradient와 방향 도함수 사이 관계가 더 잘 이해될 것이다.
참고로 사이트의 $\vec u$ 와 Gradient의 사잇각은 $\theta$ 로 표기 돼 있고, 그 단위가 $\pi$ 가 아니고 그냥 정수 값으로만 나와 있다.
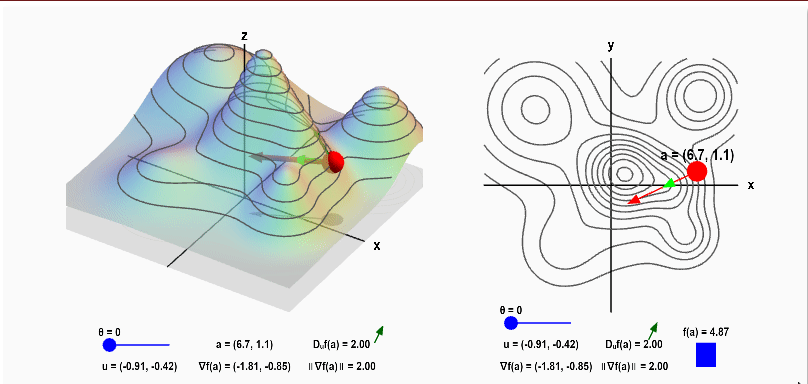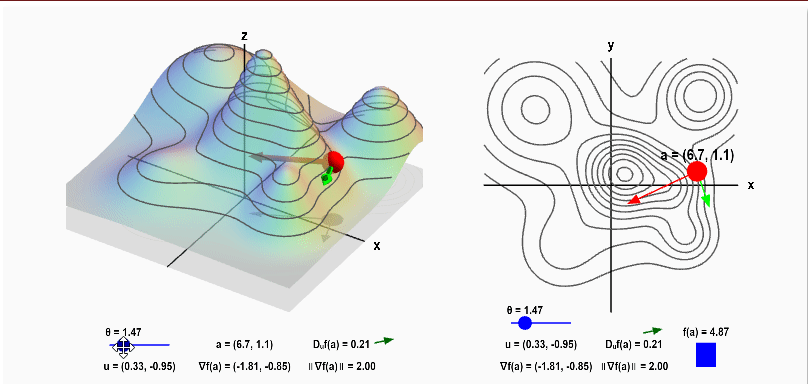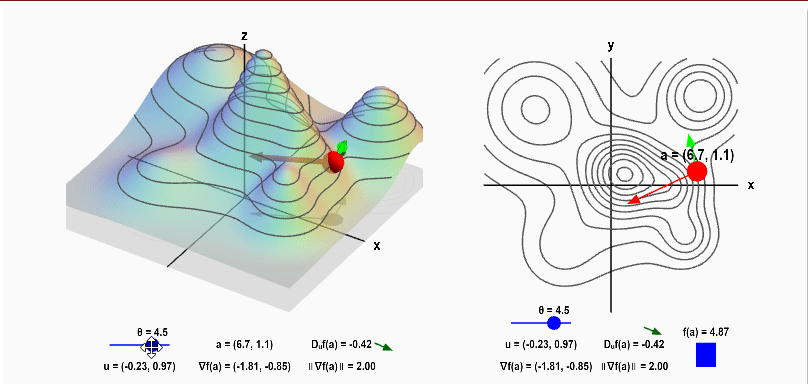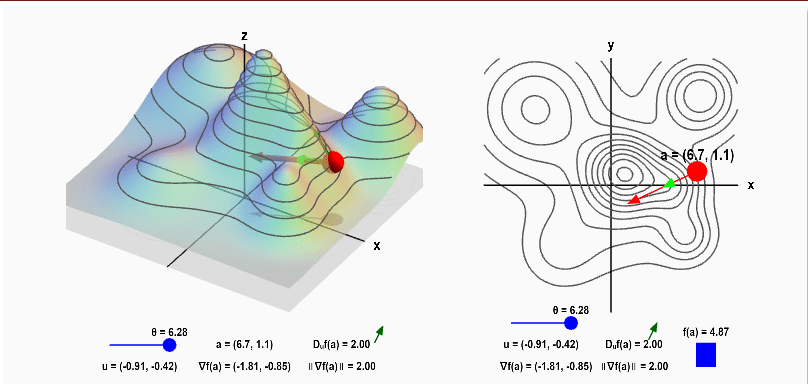
Applet: Gradient and directional derivative on a mountain - Math Insight
Applet: Gradient and directional derivative on a mountain The height of a mountain range described by a function $f(x,y)$ is shown as surface plot in three-dimensions (left) and a two-dimensional level curve plot (right). In each panel, a red point can be
mathinsight.org
참고
방향도함수는 도대체 뭘까?
먼저 방향도함수의 개념은 쉽게 말해 순간기울기를 구하는 도함수입니다! 그런데 2차원에서 배운 도함수하고는 약간 다릅니다. 아래 그림을 봅시다 2차원 상에서 그래프가 있을 때 기울기란 y의
basic-theory.tistory.com
- 방향 도함수를 기하적으로 이해하는데 도움을 받은 사이트이다.
Applet: Gradient and directional derivative on a mountain - Math Insight
Applet: Gradient and directional derivative on a mountain The height of a mountain range described by a function $f(x,y)$ is shown as surface plot in three-dimensions (left) and a two-dimensional level curve plot (right). In each panel, a red point can be
mathinsight.org
- Gradient와 방향 도함수 사이 관계를 확인할 수 있다.
12.6: Directional Derivatives
Partial derivatives give us an understanding of how a surface changes when we move in the x and y directions. But what if we didn't move exactly in x or y directions? Partial …
math.libretexts.org
- 방향 도함수, 편미분 등을 참고 했다.
