[논문 리뷰] Neural Collaborative Filtering

 

 

1. 등장 배경

---

기존 collaborative filtering(협업 필터링)에서 활용되는 Matrix Factorization은 유저 - 아이템 행렬을

각각 유저, 아이템 임베딩으로 분해한 뒤 이를 해당 유저와 아이템의 look-up table로 삼는다. 

이 경우 유저 - 아이템 행렬의 예측 값을 dot product로 구할 수 있으며 $M{\times}N$ 행렬을 $M{\times}K$, $K{\times}N$로 분해할 수 있다. 

 

https://medium.com/@connectwithghosh/simple-matrix-factorization-example-on-the-movielens-dataset-using-pyspark-9b7e3f567536

 

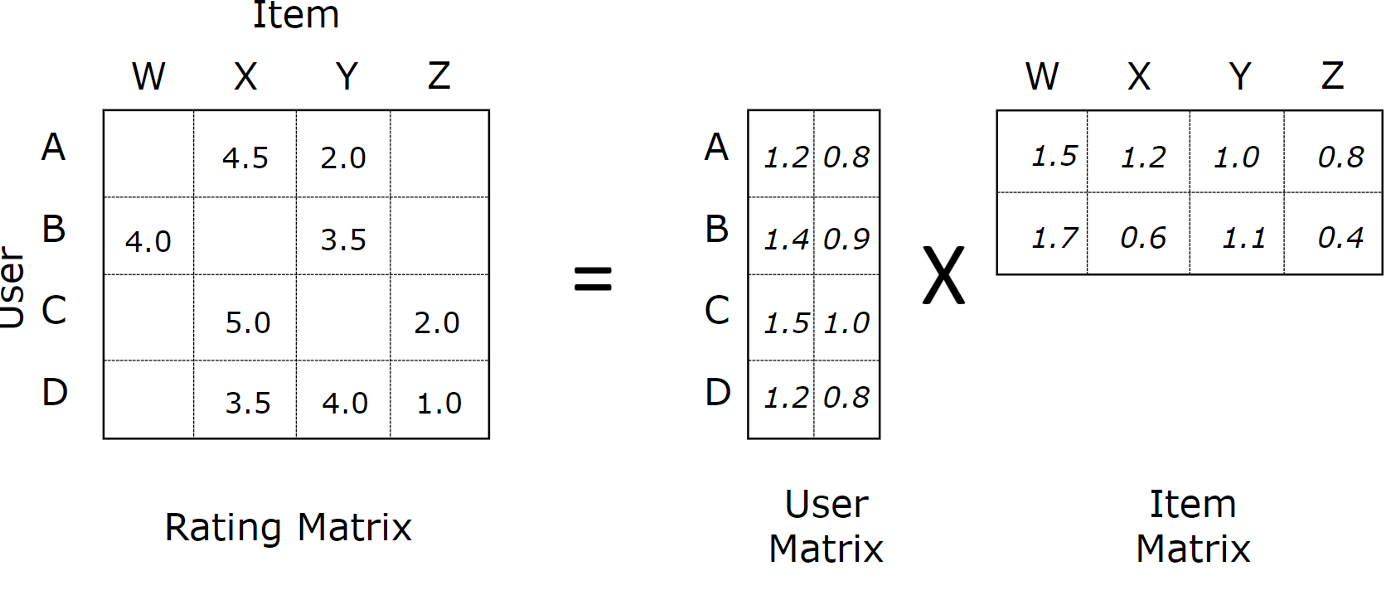
하지만 dot product는 linear한 연산이면서 동시에 모든 차원의 가중치를 동일하게 생각하기 때문에 복잡한 유저 - 아이템 행렬을 표현하기엔 충분하지 않다.

 

실제로 dot product가 활용될 latent space의 상황을 가정해보자. $u_4$의 경우 유저 - 아이템 행렬에선 $u_1, u_3, u_2$순으로 가장 유사했지만 latent space 내에선 어느 곳에 위치하더라도 $u_1, u_2, u_3$순으로 유사도 순서가 변경된다. 이는 유저 - 아이템 행렬을 latent space가 잘 반영하지 않았음을 말한다. 

 

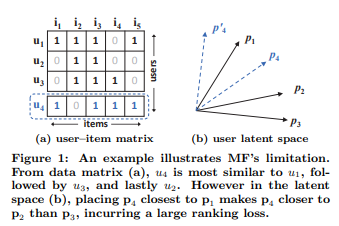
물론 이 문제는 latent space가 기존 유저 - 아이템 행렬을 잘 반영하지 않은 것이기 때문에 차원 $K$를 높게 잡으면 해결할 수 있을 것이다. 하지만 이는 곧 과대 적합으로 이어져 또 다른 문제를 발생시킨다. 또한 $K$가 높아지면 $M, N$의 값이 매우 큰 추천 시스템 특성 상 결국 파라미터 수가 그만큼 많아진다는 문제도 생긴다.  

 

따라서 기존 MF에서 사용해온 낮은 $K$로 얻은 latent space에선 dot product만으론 유저 - 아이템 행렬을 충분하게 표현할 수 없다.

 

2. 제안

---

결국 근본적으로 문제를 해결하기 위해선 $K$에 집중하기 보다는 유저 - 아이템 행렬에 대한 표현력을 올리는 것이 중요하다. 따라서 논문에선 기존 linear한 dot product로 유저 - 아이템 행렬을 예측하는 것 대신 non-linearity를 활용해 유저 - 아이템 행렬을 예측하려고 한다.

 

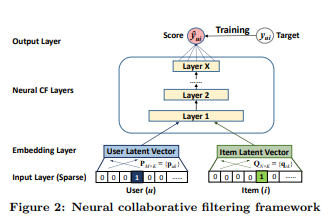
이때 그림에서 알 수 있듯이 유저, 아이템 latent space는 여전히 추출된다. 다만 이를 look-up table로 삼아 dot product하여 바로 행렬 예측에 활용하는 것이 아니고 latent space를 concat하여 layer를 순차로 통과시킨다. 이를 통해 예측에 non - linearity 특성이 확보될 것이다. 이 과정을 식으로 표현하면 다음과 같다.

 

$$f\left(\mathbf{P}^{T} \mathbf{v}_{u}^{U}, \mathbf{Q}^{T} \mathbf{v}_{i}^{I}\right)=\phi_{\text {out }}\left(\phi_{X}\left(\ldots \phi_{2}\left(\phi_{1}\left(\mathbf{P}^{T} \mathbf{v}_{u}^{U}, \mathbf{Q}^{T} \mathbf{v}_{i}^{I}\right)\right) \ldots\right)\right)$$

 

논문에선 앞서 본 모델의 구조를 굳이 NCF Framework라고 이름 지었다. 이는 해당 Framework의 기본 틀을 유지하면서 Layer만 변경하면 기존 Matrix Factorization과 논문에서 제안한 GMF(Generalized Matrix Factorization), MLP(Multi-Layer  Perceptron)를 구성할 수 있기 때문이다. 또한 GMF와 MLP를 합쳐 NeuMF도 구성할 수 있다.

 

$$\hat{y}_{u i}=a_{\text {out }}\left(\mathbf{h}^{T}\left(\mathbf{p}_{u} \odot \mathbf{q}_{i}\right)\right)$$

 

해당 Framework를 식으로 간단히 표현하면 위 식과 같다. $a_{out}$은 활성화 함수이며 $h$는 모델 가중치이다.

이때, $h$의 값을 모두 1로 설정하고 $a_{out}$을 identity function으로 설정한다면 자연스럽게 MF가 될 것이다. GMF와 MLP, NeuMF는 각각 다음과 같다. 이때, NeuMF는 가중치 $\alpha$를 0.5로 설정하였다. 

 

GMF

$$\hat{y}_{u i}={\sigma}\left(\mathbf{h}^{T}\left(\mathbf{p}_{u} \odot \mathbf{q}_{i}\right)\right)$$

MLP

$$\begin{aligned} \mathbf{z}_{1} &=\phi_{1}\left(\mathbf{p}_{u}, \mathbf{q}_{i}\right)=\left[\begin{array}{c}\mathbf{p}_{u} \\ \mathbf{q}_{i}\end{array}\right] \\ \phi_{2}\left(\mathbf{z}_{1}\right) &=a_{2}\left(\mathbf{W}_{2}^{T} \mathbf{z}_{1}+\mathbf{b}_{2}\right) \\ & \ldots \\ \phi_{L}\left(\mathbf{z}_{L-1}\right) &=a_{L}\left(\mathbf{W}_{L}^{T} \mathbf{z}_{L-1}+\mathbf{b}_{L}\right) \\ \hat{y}_{u i} &=\sigma\left(\mathbf{h}^{T} \phi_{L}\left(\mathbf{z}_{L-1}\right)\right) \end{aligned}$$

NeuMF

$$\hat{y}_{u i}=\sigma\left(\mathbf{h}^{T}\left[\begin{array}{l}\phi^{G M F} \\ \phi^{M L P}\end{array}\right]\right)$$

$$\mathbf{h} \leftarrow\left[\begin{array}{c}\alpha \mathbf{h}^{G M F} \\ (1-\alpha) \mathbf{h}^{M L P}\end{array}\right]$$

​

이때, 모델의 출력이 모두 $\sigma$를 통과함을 알 수 있다. 이를 통해 Framework의 objective가 결국 binary - classification을 해결하는 것임을 알 수 있다.

Framework는 loss를 pair-wise loss가 아닌 point-wise loss로 설정했다. 이때 기존에 point-wise loss를 사용한 다른 implicit 추천 시스템에선 다음과 같은 squared loss를 활용했다. 이때 $y$와 $y^{-}$는 각각 확인된 interaction과 negative instances(negative sampling)이다. 

$$
L_{s q r}=\sum_{(u, i) \in \mathcal{y}\cup y^{-}} w_{u i}\left(y_{u i}-\hat{y}_{u i}\right)^{2}
$$

 

하지만 이는 확률적 관점에서 보면 옳지 않다. MLE 관점에서 보면 sqaured loss는 결국 label이 gaussain distribution이라는 조건을 만족해야 한다. 하지만 implicit 데이터는 label이 0과 1로 결국 오히려 bernoulli distribution을 만족함을 알 수 있다.

 

따라서 저자는 bernoulli distribution하 최적의 모델을 구하기 위해서 binary-cross-entropy loss(log-loss)를 사용했다.

loss를 유도하는 과정은 다음과 같다. 추가로 sqaured loss와 cross-entropy가 왜 각각 gaussain과 bernoulli distribution을 가정하는 지 알 수 있는 사진도 첨부한다.

 

 

오토 인코더의 모든 것 - 1

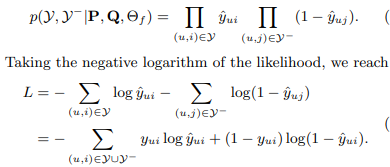
3. Neural matrix factorization model(NeuMF)

---

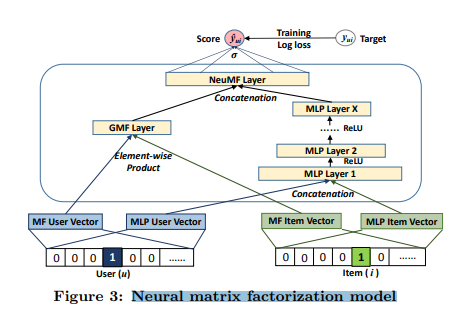
앞서 언급했듯이 NeuMF는 GMF와 MLP를 결합해서 얻을 수 있다. 이를 통해 GMF의 linear한 특성을 MLP의 non-linear한 특성과 결합할 수 있을 것이다. 이때 GMF와 MLP의 latent space를 동일하게 설정할 수도 있지만 GMF(linear)와 MLP(non - linear)의 다른 성질을 고려해 각각 따로 latent space를 구성한다.

 

NeuMF를 처음부터 학습하는 대신 GMF와 MLP 각각을 Adam으로 pretrain 시킨 후 활용한다. 이때, NeuMF에 합쳐질 GMF와 MLP 각각 다른 momentum state를 가지고 있기 때문에 NeuMF를 학습시킬 땐 vanila SGD를 통해서 진행한다.

 

4. 결과 확인

---

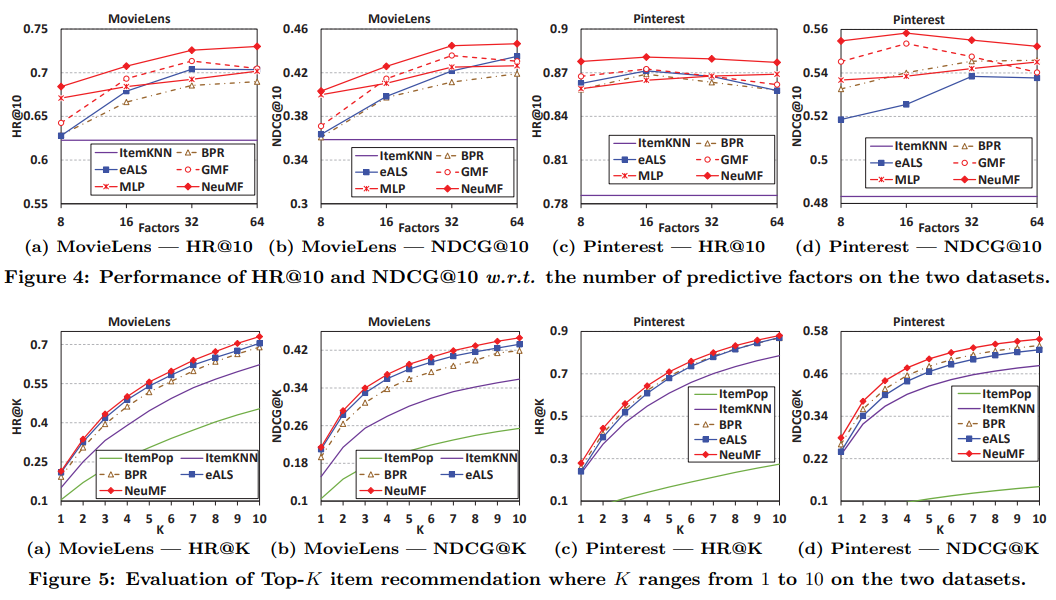
MLP와 GMF를 결합한 NeuMF가 가장 높은 성능을 기록했으며 이는 MLP(linear)와 GMF(non - linear)결합한 시도가 성공적이었음을 의미한다.  또한 MLP와 GMF도 높은 성능을 기록했는데 이는 제안한 Neural Collaborative filtering Framework 자체가 좋다는 것을 의미한다.

• Framework : log loss(binary-cross entropy)와 negative sampling을 기반으로 유저 - 아이템 행렬을 non - linear하게 학습 가능

 

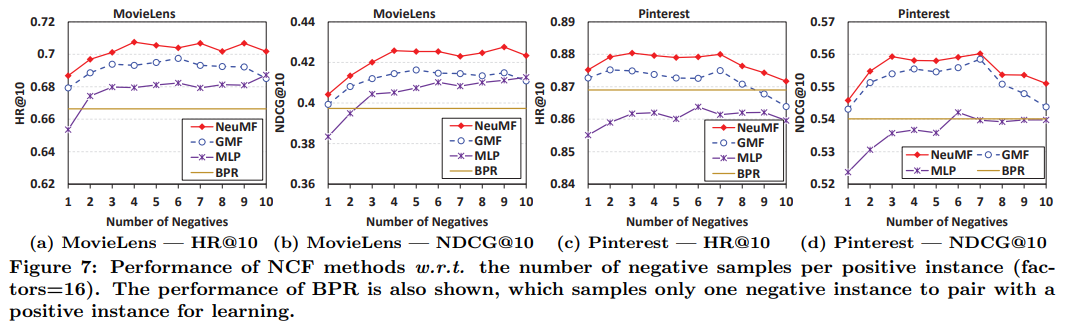
제안한 log loss는 pair-wise loss와 비교했을 때 negative sampling의 수를 조절할 수 있고 이를 통한 성능 향상도 기대할 수 있다는 상대적 장점이 있다. 실제로 BPR과 동일하게 1개의 negative sample만을 가지고 학습했을 땐 성능이 더 낮았지만 샘플 수를 늘림에 따라 성능이 더 좋아지는 경우도 존재했다.  

 

제안한 Framework는 log loss와 negative sampling을 기반으로 유저 - 아이템 행렬 표현을 non - linear 하게 학습이 가능하다.

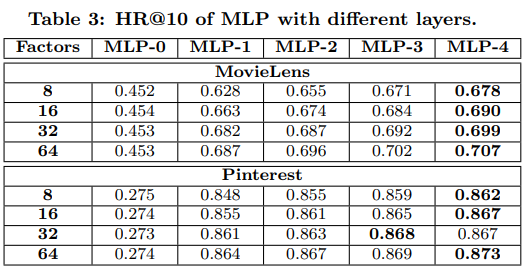
Framework의 우수성은 실험을 통해 확인했다. 그럼 MLP 모델처럼 layer 자체에서 ReLU(activiation)를 통해 non-linearity를 추가하는 딥러닝 구조가 정말 추천에 도움이 되는지도 확인할 필요가 있다. 이를 위해 MLP layer를 늘려가며 성능을 확인했고 MLP layer가 늘어날 수록(non-linearity가 증가할 수록)성능이 증가함을 확인했다.

---

참고

Neural Collaborative Filtering