[논문 리뷰] Transformer : Attention Is All You Need

https://arxiv.org/pdf/1706.03762.pdf

1. 등장 배경

---

기존 sequence transduction(machine translation)에서 활용된 seq2seq 모델은 순차적으로 입력(sequence position $t$)을 받아 처리

 

seq2seq는 순차적으로 입력을 받아 간단하게 sequence를 표현할 수 있지만 long-range dependencies, parallelizable 문제가 발생

 

long-range dependencies를 해결하기 위해서 Attention을 도입했지만 fixed-encoder representation으로 context를 온전히 표현할 수 없는 seq2seq의 근본적인 문제는 해결 불가

 

2. 제안

---

입력을 순차적으로 처리하는 RNN을 버리고 Attention만을 사용한 Encoder - Decoder 구조를 도입해 long-range dependencies와 parallelizable 문제를 해결. 이때 position을 반영할 수 있도록 sinusodal function을 활용한 Positional Encoding을 도입해 문장을 한꺼번에 입력

 

Parallelizable

• 병렬 처리 가능한 특성을 활용하면서 동시에 different representation sub-spaces를 얻기 위해서 Multi-Head Attention 사용
• 병렬 처리에 유용한 dot - product Attention을 큰 $d_k$에서도 빠른 속도로 활용할 수 있도록 Attention 값을 $\sqrt{d_k}$로 scaling

Long-range dependencies

• encoder, decoder에서의 self-attention과 encoder - decoder 사이 attention 도입
• decoder 시점에서 미래 단어(아직 모르는 단어까지 한꺼번에 입력)들을 참조하지 못하도록 look-ahead mask 도입

학습 관련

• residual-connection과 layer-normalization 도입
• ReLU를 가진 Position-wise Feed-Forward Network를 통해 비선형성 증가(1 x 1 conv와 비슷한 역할)
• input, output을 통해 공유된 embedding representation 학습
• scale variant한 $softmax$에서 gradient vanishing을 방지하기 위해서 Attention 값을 $\sqrt{d_k}$로 scaling

 

3. 모델 구조

---

https://arxiv.org/pdf/1706.03762.pdf

논문은 Encoder, Decoder 모두 6개씩 쌓은 Transformer

Attention

https://arxiv.org/pdf/1706.03762.pdf

 

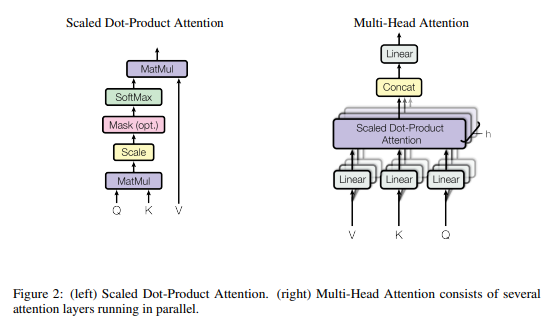
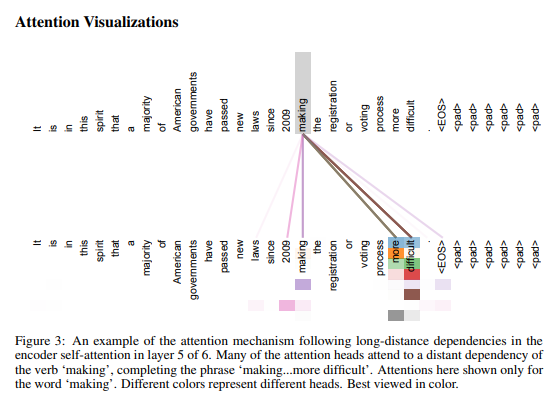
$\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V$

 

$Q$는 물어보는 주체이며 $K$는 $Q$와 비교가 되는 대상

$Q$, $K$ 사이 유사도를 dot-product을 통해 얻은 뒤 이를 $softmax$하여 확률 값으로 정규화

유사도 확률 값과 V를 dot-product 하여 유사도가 높은 단어에만 주목

Self-Attention : Q, K, V가 Encoder/Decoder 내 단어들
Encoder-Decoder Attention : Q는 Decoder  / K, V는 Encoder 내 단어들

 

앞선 과정을 병렬화 하면서 동시에 다양한 different-representation sub-spaces를 얻기 위해서 

$h$ Multi-Head Attention 진행

 

논문에선 $h$ = 8, $d_{model}$ = 512, $d_k, d_v, d_q$ = 64로 설정.

 

\[\mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ...,
\mathrm{head_h})W^O    \\
    \text{where}~\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i)\]

$W_i^Q \in \mathbb{R}^{d_{model} \times d_k}, \ W_i^K \in \mathbb{R}^{d_{model} \times d_k}, \ W_i^V \in \mathbb{R}^{d_{model} \times d_v}$

 

 

Why Self-Attention?

https://arxiv.org/pdf/1706.03762.pdf

1. Time Complexity

일반적으로 $d$가 $n$보다 더 크기 때문에 낮은 $O$

만약 $n$이 너무 큰 경우 Self-Attention 참고 시 주위 $r$개의 단어만 참고하여 줄일 수 있음

 

2. Parallelizability

입력을 순차적으로 받지 않고 한번에 받기 때문에 $O(1)$의 복잡도

병렬화에 유리

 

3. Maximum Path Length

long-range dependices에 활용될 Attention을 얻기까지 필요한 시간

RNN의 경우 $n$의 입력이 끝나야지만 참고할 수 있음

Self-Attention은 입력을 통해 바로 확인 가능하기 때문에 $O(1)$

 

Look - Ahead Mask

https://pozalabs.github.io/transformer/

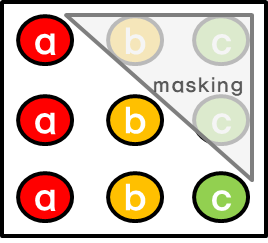
Decoder에서는 Encoder와 달리 순차적으로 결과를 만들어내야 함

Self-Attention을 처리할 때 Masking을 통해 해당 position 보다 이후에 있는 position에 attention을 주지 못하게 함

 

Positional Encoding

https://kazemnejad.com/blog/transformer_architecture_positional_encoding/

 

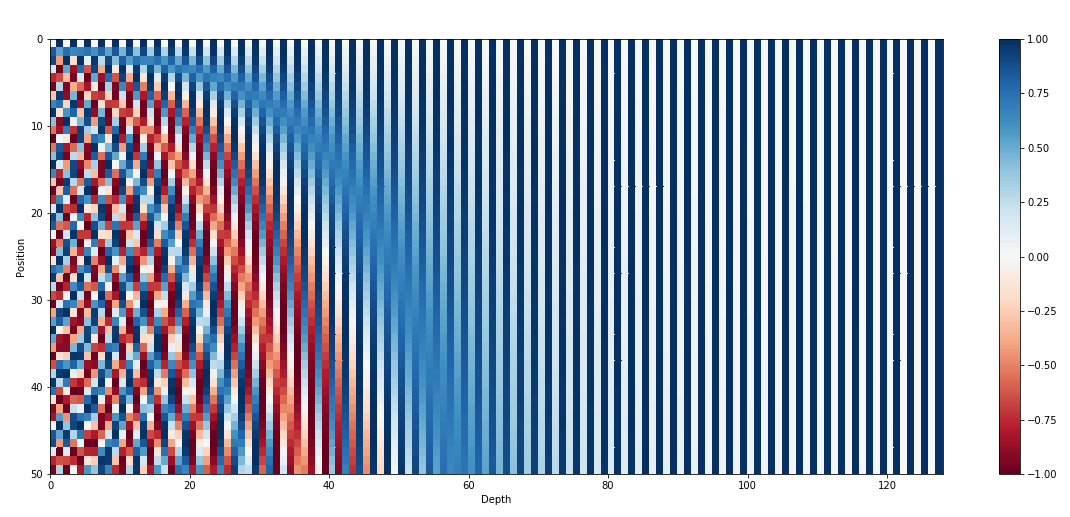
\[PE_{(pos, 2i)} = sin(pos / 10000^{2i / d_{model}})\]

\[PE_{(pos, 2i+1)} = cos(pos / 10000^{2i / d_{model}})\]

 

 

Attention 만으로 Sequence 정보를 담아내기 위해서 sinusoidal function 활용

따라서 동일 dimension($i$)에 놓이더라도 position($pos$)에 따라 다른 의미

+ 가설 : $PE_{pos+k}$는 $PE_{pos}$의 linear function으로 표현되기 때문에 모델이 relative position을 학습하기 더 쉬울 것

 

vs Positional Embedding ?

둘 사이의 성능 차이는 없었음

하지만 inference 상황에서 embedding은 훈련에 사용된 sequence보다 더 긴 sequence가 입력됐을 시 처리할 수 없지만 encoding은 연산량이 늘어나긴 하지만(더 많은 postion 확인) 처리할 수 있기 때문에 선택

 

 

4. 결과

---

https://arxiv.org/pdf/1706.03762.pdf

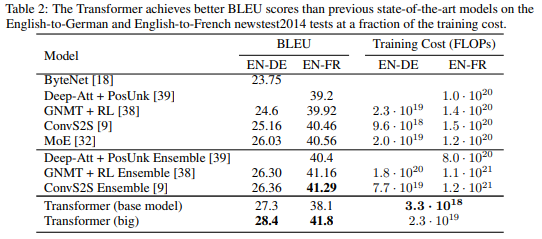
병렬화로 Training Cost를 매우 줄이면서도 sequence transduction에서 SOTA급 성능 달성

---

참고

The Illustrated Transformer

 

• Transformer 전반적인 과정을 그림으로 확인할 수 있다.

Transformer Networks: A mathematical explanation why scaling the dot products leads to more stable…

 

• Scaled Dot-product의 필요성에 대해서 확인할 수 있다.

Transformer Architecture: The Positional Encoding - Amirhossein Kazemnejad's Blog

• Positional Encoding에 대해서 확인할 수 있다.