
시간복잡도
알고리즘을 위해 필요한 연산의 횟수를 나타냄
코딩 테스트에서 작성한 프로그램이 모든 입력을 받아 처리하고 실행한 결과를 출력하는데까지 걸리는 시간 측정
특정한 크기의 입력에 대해 알고리즘이 얼마나 오래 걸리는 지를 나타냄
- 문제에서 가장 먼저 확인
- ‘복잡도’라고 하면 보통 ‘시간 복잡도’를 의미
- 보통 코딩 테스트의 시간 제한 : 1 ~ 5초 / 파이썬 기준 대략 2000만번의 연산 ~ 1억번의 연산 처리 가능
시간 제한 문제를 해결할 때는 N의 범위에 따라 다른 시간 복잡도 알고리즘을 설계
시간 제한이 1초에 대한 문제에 대한 예시
| N의 범위 | 복잡도 |
| 500 | O(N3) |
| 2,000 | O(N2) |
| 100,000 | O(NlogN) |
| 10,000,000 | O(N) |
공간 복잡도
알고리즘을 위해 필요한 메모리의 양
보통 128MB ~ 512MB의 공간 복잡도 제한이 있음
- 데이터의 개수가 1000만 단위가 넘어가지 않도록 설계 필요
- 파이썬에서도 100만개 이상 크기의 리스트를 선언하는 경우는 거의 없음
Big - O
복잡도 표기법
차수가 가장 큰 항만 고려하지만 경우에 따라 상수를 고려해야할 수도 있음
복잡도 별 명칭은 다음과 같음

다양한 자료구조와 정렬 알고리즘의 시간 복잡도는 다음과 같음


피보나치 함수
- 재귀로 접근할 경우
- Ω(2n/2)의 시간 복잡도
def fibo(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibo(n - 1) + fibo(n - 2)- 실행 과정과 시간 복잡도 계산 과정

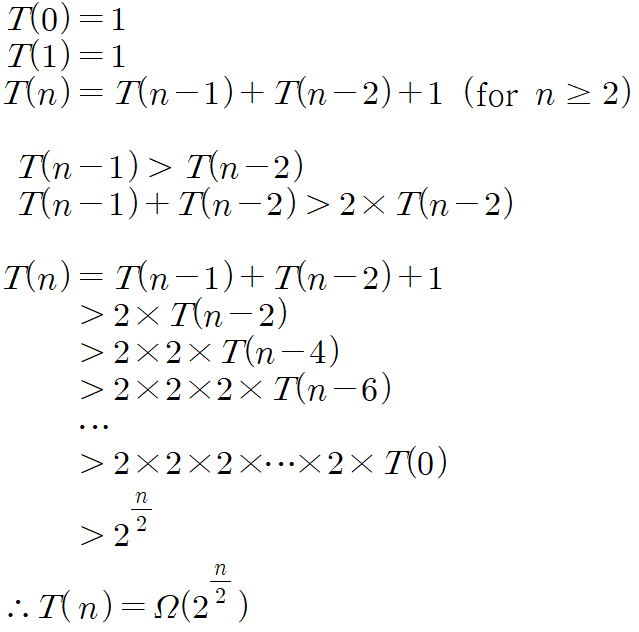
- memoization(메모이제이션) 활용 시
- 시간 복잡도를 O(N)으로 줄일 수 있음
answer = [0, 1]
for i in range(2, 100001):
answer.append(answer[i - 2] + answer[i - 1])파이썬 함수
- bin() : logN
참고
https://www.bigocheatsheet.com/
이것이 취업을 위한 코딩테스트다
