Intro
지도 학습 모델의 성능을 확인할 때는 과대 적합이나 과소 적합 여부를 정확하게 파악해야, 올바른 방법으로 모델을 개선할 수 있습니다. 과대 적합, 과소 적합은 Bias(편향)와 Variance(분산)과 깊은 관련이 있기 때문에 우선 편향과 분산을 이해하는 것이 중요합니다. 이번 포스팅에선 편향과 분산을 이해를 돕기 위한 내용을 정리했습니다.
Bias - Variance?

먼저 그림을 통해서 편향과 분산에 대해서 이해해 봅시다. 그림에선 과녁의 중심과 다트 사이의 거리가 멀면 편향이 높다고 합니다. 또한 각 다트 사이의 거리가 멀게 되면 분산이 크다고 말합니다.
다트를 던지는 행위를 예측이라고 해봅시다. 이때 각 다트들의 위치는 곧 예측값이, 과녁의 중심은 실제값이 됩니다. 이를 통해 편향과 분산을 다음과 같이 이해할 수 있습니다.
편향 : 실제값과 예측값 사이 차이를 나타내는 지표
분산 : 예측값들이 얼마나 퍼져 있는 지에 대한 지표
편향과 분산에 대해 이해한 뒤 다시 위의 그림을 보면, 편향과 분산이 모두 작은 경우 바람직한 경우라고 생각할 수 있습니다. 과녁과 가까우면서도 흩어져 있지도 않기 때문입니다.
하지만 아쉽게도 편향과 분산을 동시에 작게하는 것은 불가능합니다. 편향이 작아지면 분산이 커지고, 분산이 작아지면 편향이 커집니다. 이처럼 편향과 분산은 Trade - Off 관계입니다. 따라서 전체 에러값을 최소화할 수 있는 수준에서 편향, 분산 값을 조절할 수 밖에 없습니다.

Bias - Variance!
회귀 모델과 평가 지표 MSE(Mean Squared Error)를 이용하면 Residual Expectation(잔차 기댓값)을 Bias와 Variance로 분해할 수 있습니다. 분해 과정을 이해하면, 편향과 분산을 이해하는데 큰 도움이됩니다. 수식을 통한 정확한 분해 과정은 동영상을 참고하면 좋습니다.
과정의 핵심을 요약하면 아래와 같습니다.
우선 훈련 데이터가 ${\displaystyle x_{1},\dots ,x_{n}}$ 와 각 ${\displaystyle x_{i}}$들에 대응되는 ${\displaystyle y_{i}}$들의 쌍으로 표현되는 점들의 집합이라고 합시다. 이 경우 각 데이터들, 즉 추출된 표본들은 피할 수 없는 노이즈를 가지고 있습니다.
따라서 $y=F^{*}(x)+\epsilon$인 관계를 가집니다. 이때 ${\displaystyle \epsilon }$ 은 평균이 0이고 분산이 ${\displaystyle \sigma ^{2}}$ 인 정규 분포를 따른다고 알려져 있기 때문에, 동일한 $x$라고 하더라도 노이즈의 영향 때문에 다른 $y$ 값을 가지게 됩니다.

우리는 결국 모든 $x$에 대해서 ${\displaystyle y}$를 최대한 잘 근사하는 함수 ${\displaystyle {\hat {F}}(x)}$를 찾고자 합니다. 여기에서 말하는 "최대한 잘"이란 정량적으로 ${\displaystyle y}$ 와 ${\displaystyle {\hat {F}}(x)}$ 사이의 MSE를 측정하여, 그 값이 가장 작은 것을 찾는 것을 의미합니다.
$$
MSE=\frac{1}{N} \sum_{i=1}^N\left(y_i - \hat {F}_i\right)^2 : 최소가 돼야 함
$$
이때 $\hat {F}(x)$는 훈련 데이터를 통해서 구하기 때문에, 훈련 데이터에 과적합 될 우려가 있습니다. 이상적인 $\hat {F}(x)$가 되기 위해선 아직 확인하지 못한 데이터에 대해서도 예측을 잘 해야하기 때문에, MSE의 일반화된 성능을 확인하는 것이 필요합니다.
이를 위해 MSE에 대한 기댓값을 확인해보면 Bias와 Variance에 대한 정보를 얻을 수 있습니다. 이 수식을 아래와 같이 정리하게 되면 MSE의 기댓값이 결국 기댓값의 MSE로 변환됨을 확인할 수 있습니다.
참고로 Mean과 기댓값은 유사해 보이지만, Mean은 실험(관측된 샘플)을 기준으로 한 지표이고, 기댓값은 표본 공간을 기준으로 한 지표라는 점에서 차이가 있습니다.
Expectation VS. Mean VS. Average 비교 완벽 정리!
아,,, 한창 MSE에서 Expectation 구해서 Bias-Variance Decomposition을 증명하려고 하는데 계속 짜...
blog.naver.com
$$
E\{M S E\}=E\left\{\frac{1}{N} \sum_{i=1}^N\left(y_i - \hat {F}_i\right)^2\right\}=\frac{1}{N} \sum_{i=1}^N E\left\{\left(y_i - \hat {F}_i\right)^2\right\}
$$
결국 각 $x_i$(샘플)에 대한 기댓값을 구하게 되면 Bias와 Variance를 확인할 수 있습니다. 과정은 생략하고 최종 식만 적으면 다음과 같습니다. 수식에서 $\bar F_i$는 모든 $\hat {F}_i$에 대한 예측 값의 평균입니다.
$$
E[F^*_i - \bar {F}_i]^2 + E[\bar {F}_i - \hat {F}_i]^2 + \sigma ^2
$$
$$
[F^*_i - \bar {F}_i]^2 + E[\bar {F}_i - \hat {F}_i]^2 + \sigma ^2
$$
$$
Bias^2(\hat {F}_i) + Var^2(\hat {F}_i) + \sigma ^2
$$
Bias - Variance는 샘플에 대한 값
여기서 중요한 점은 Bias와 Variance가 한 샘플($x$)에 대한 값이고, 이 값들을 MSE 하여 전체 샘플에서의 Bias와 Variance를 구할 수 있다는 것입니다. 한 $x$에 대한 Bias와 Variance는 아래 그림과 같고 이를 모든 $x$에 대해 계산하여 MSE를 구하면 결국 전체 Bias와 Variance를 얻을 수 있습니다.

위 그림과 수식을 통해 확인할 수 있는 것이 하나 더 있습니다. $F^*$ 즉, 실제 값에 대한 예측을 얼마나 잘 했는지를 알 수 있게 해주는 지표가 바로 Bias이고 Variance는 각 예측의 분포만을 알 수 있다는 점입니다. 실제로 Variance term엔 $F^*$에 대한 정보가 없습니다.
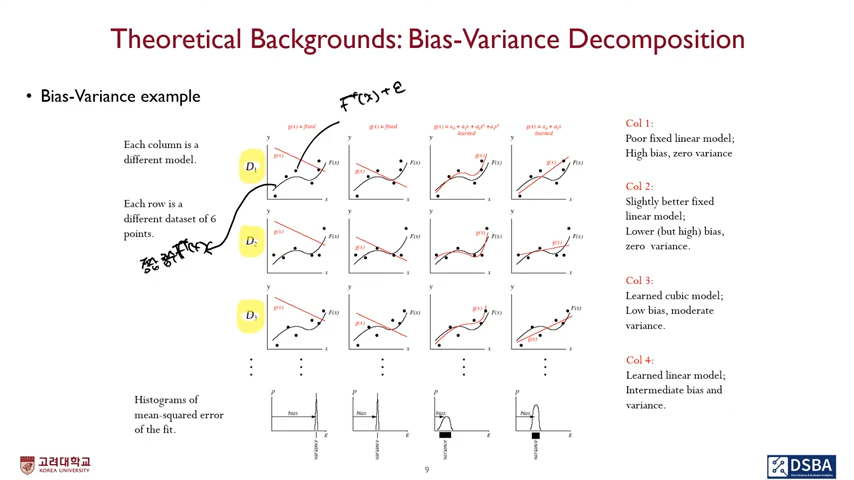
위 그림엔 각 데이터 별 $\hat {F}_i$와 $F^*$ 사이 관계가 나와있는데, 이해하는데 도움이 될 거 같아서 추가했습니다. 실제 $F^*$를 검은색 실선, 노이즈에 의한 관측치인 $F^* +\epsilon$를 검은 점으로 표현했습니다. 이에 대한 근사 함수는 $\hat {F}_i$으로 빨간 실선으로 표현됐습니다.
각 $x$에 대한 Bias와 Variance를 확인하면 이전 그림과 같고, 최종적으로 $Bias^2(\hat {F}_i) + Var^2(\hat {F}_i) + \sigma ^2$에 대한 MSE 값을 구하면 위와 같습니다.
참고
Bias–variance tradeoff - Wikipedia
From Wikipedia, the free encyclopedia Property of a model A function (red) is approximated using radial basis functions (blue). Several trials are shown in each graph. For each trial, a few noisy data points are provided as a training set (top). For a wide
en.wikipedia.org
- 편향 - 분산의 정의를 이해하는데 도움을 받았다.
바이어스(Bias) / 분산(Variance) 용어 완벽 이해!
아,,, 드디어 완벽하게 정리되었다. 이놈의 바이어스와 분산이런 녀석들... 나름대로 정리한 내용을 최대한...
blog.naver.com
- 편향 - 분산을 쉽게 설명해주는 블로그다.
04-2: Ensemble Learning - Bias-Variance Decomposition (앙상블 - 편향과 분산)
- 편향 - 분산 분해 과정을 확인할 수 있다.
