Regression Metrics(회귀 평가 지표) 알아보기 : MSLE, RMSLE, R^2, MAPE, sMAPE, MPE

어떤 특성을 가진 Regression Metrics(회귀 평가 지표)?

---

기존에 다뤘던 MAE, MSE, RMSE는 Scale-Dependent한 특성이 있었다. 하지만 이 포스팅에서 다룰 지표들은 비율, % 기반으로 접근하기 때문에 상대적으로 Scale에서 자유롭다는 특징이 있다.

 

MSLE(Mean Sqaured Log Error)

---

$$ MSLE = \frac{1}{n}\sum_{i=1}^{n}(\log{y_i}-\log{\hat{y_i})}^2 $$

• 모델의 예측 $\hat{y}$와 Label $y$에 각각 Log를 적용해 MSE를 한 것이다.

Log 그래프의 양상

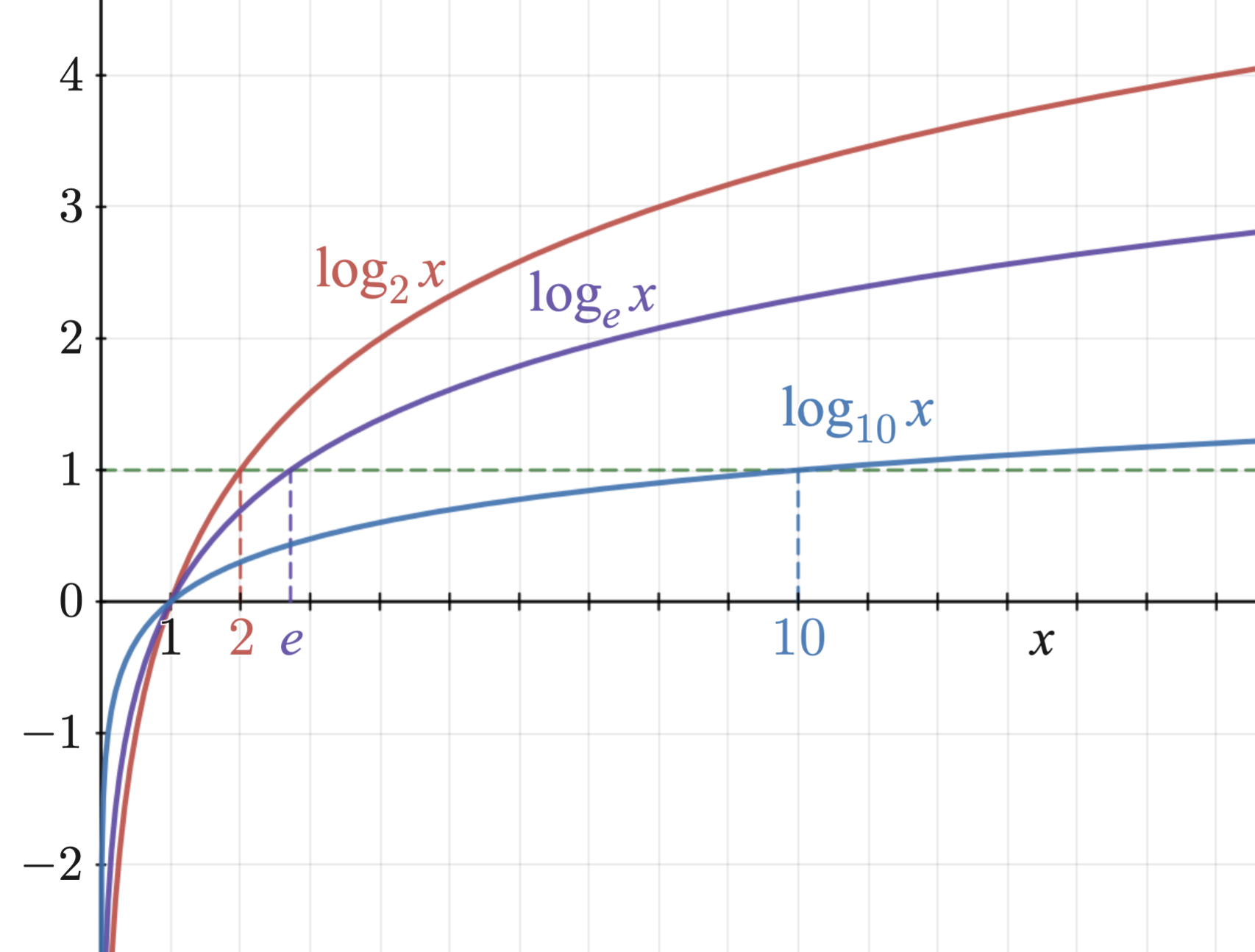
• Log 함수의 특성을 가지고 있는 지표이다.
  • $\log{y}-\log{\hat{y}} = \frac{\log{y}}{\log{\hat{y}}}$ 이기 때문에 상대적 차이를 측정할 수 있다.
  • Log로 정규화 했기 때문에 Outlier(이상치)에 덜 민감하다.
    • Log 함수는 값이 커질 수록 변화율이 작다.
  • Under-estimation에 패널티를 부여한다.
    
    • $\hat{y}$가 분모에 있기 때문!

 

RMSLE(Root Mean Squared Log Error)

---

$$ RMSLE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(\log{y_i}-\log{\hat{y_i}})^2} $$

• 모델의 예측 $\hat{y}$와 Label $y$에 각각 Log를 적용해 RMSE를 한 것이다.
• MSLE와 유사한 특성을 가진다.

 

$R^2$(결정 계수, Coefficient of Determination)

---

$$ R^2 = \frac{\sum(\hat{y_i}-\bar{y})^2}{\sum(y_i-\bar{y})^2} $$

• $y$의 전체 분산 중, 모델 예측 $\hat{y}$를 통해 설명할 수 있는 Variance(분산)의 비율을 나타낸 수치이다.
  • 0 ~ 1 사이의 값을 가지기 때문에 대략적인 성능 비교 시 도움이 된다.
• Bias(편향)에 대한 정보가 없기 때문에, 지표만 보고 판단할 경우 Overfitting(과적합)이 발생할 수 있다.

 

MAPE(Mean Absolute Percentage Error)

---

$$ MAPE=\frac{1}{n}\displaystyle\sum_{i=1}^{n} |\frac{y_i-\hat{y}_i}{y_i}| $$

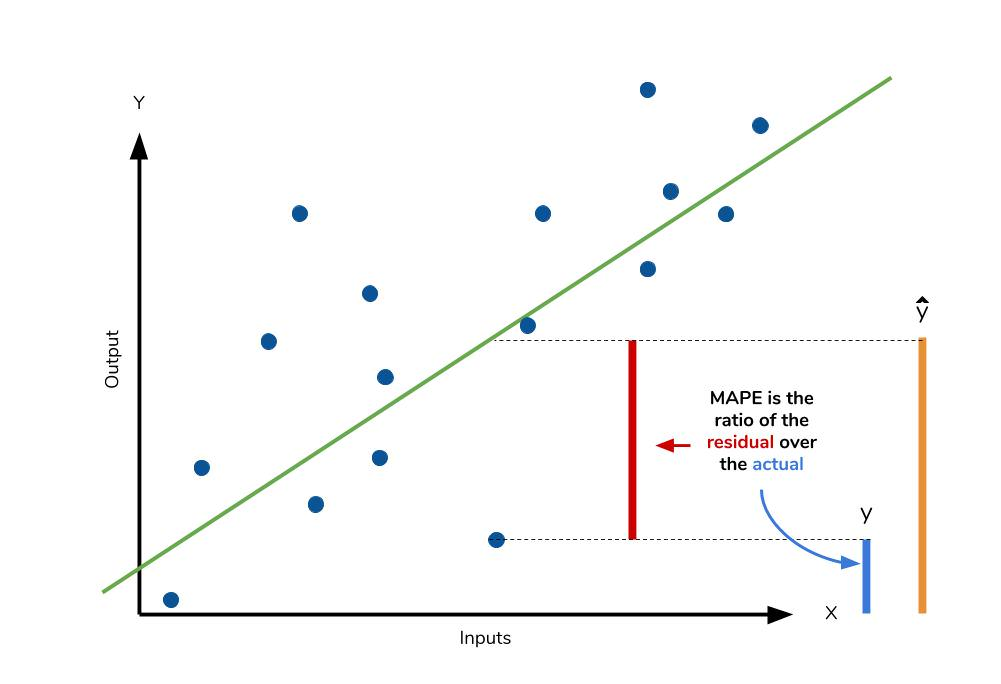
• MAE와 유사한 형태로 Residual(잔차)을 Label $y$의 Scale로 나눠 % 단위로 표현할 수 있다.
  • $y$로 나눠주기 때문에 $y = 0$ 인 경우 계산이 불가능하고, $y$가 0에 가까운 작은 값일 때 수치가 매우 커진다는 특징이 있다.
  • $y$로 나눠주기 때문에 Scale에도 영향 받는다.
• $\hat{y}$와 $y$의 대소 관계에 영향을 받는다.
  • Over-estimation일 경우 패널티를 부여한다.

 

sMAPE(symetric Mean Absolute Percentage Error)

---

$$ sMAPE=\frac{100}{n}\displaystyle\sum_{i=1}^{n} \frac{|y_i-\hat{y}_i|}{|y_i| + |\hat{y}_i|} $$

• $\hat{y}$와 $y$의 대소 관계에 영향을 받지 않도록 분모에 $\hat{y}$을 추가했다.
• $\hat{y}$를 Under-estimation할 경우 분모가 더 작아져 패널티를 부여한다.

# y^, y 사이 대소 관계 영향 X -> 두 식의 sMAPE 결과가 같음
TRUE_UNDER = np.array([10, 20, 30, 40, 50])
PRED_OVER = np.array([30, 40, 50, 60, 70])

TRUE_OVER = np.array([30, 40, 50, 60, 70])
PRED_UNDER = np.array([10, 20, 30, 40, 50])

# Under-estimation에 패널티
TRUE2 = np.array([40, 50, 60, 70, 80])
PRED2_UNDER = np.array([20, 30, 40, 50, 60])
PRED2_OVER = np.array([60, 70, 80, 90, 100])

 

MPE(Mean Percentage Error)

---

$$ MPE=\frac{1}{n}\displaystyle\sum_{i=1}^{n} \frac{y_i-\hat{y}_i}{y_i} $$

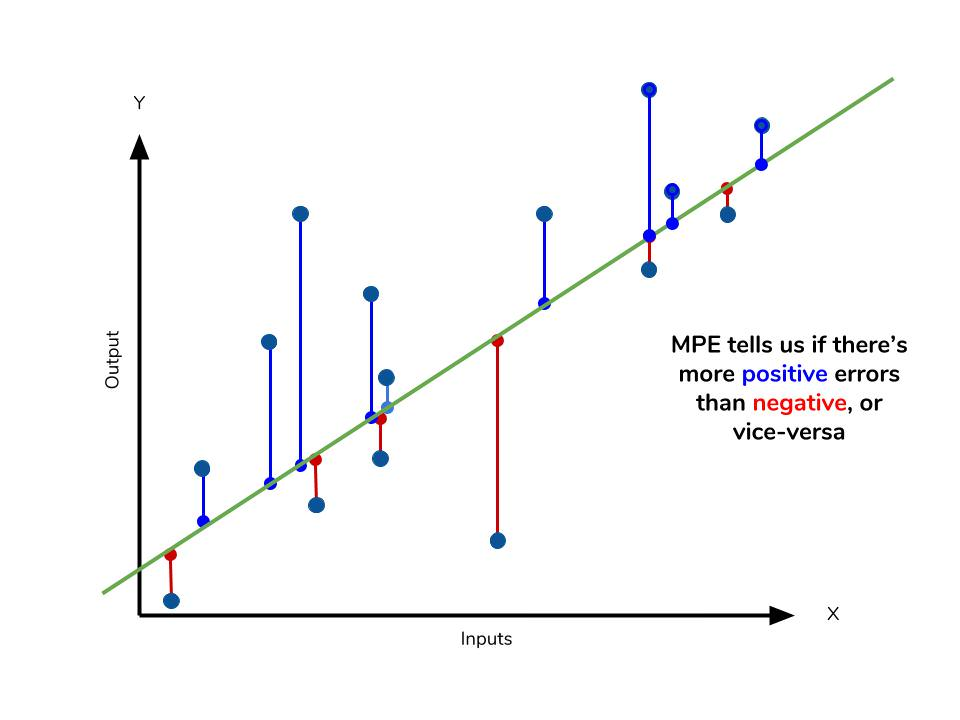
• MAPE 식에서 절댓값을 제외했다.
  • 부호가 그대로 유지되기 때문에 Under/Ove Estimation 여부를 판단할 수 있다는 장점이 있다.

---

참고

Regression 모델 평가 방법

A Comprehensive Overview of Regression Evaluation Metrics | NVIDIA Technical Blog

1. Time Series 소개 — PseudoLab Tutorial Book